Class 9 Mathematics MCQ Triangles with Answers is Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 9 Mathematics MCQ Triangles with Answers to know their preparation level.
Students who are searching for NCERT Class 9 Mathematics MCQ Triangles with Answers are compiled here to get good practice on all fundamentals. Know your preparation level on MCQ Questions for Class 9 Mathematics MCQ Triangles with Answers. You can also verify your answers from the provided Class 9 Mathematics MCQ Triangles with Answers. So, ace up your preparation with MCQ of Class 9 Mathematics MCQ & NCERT Textbook solutions Examinations.
NCERT Class 9 Mathematics MCQ Triangles with Answers
Question :D is a Point on the Side BC of a △ABC such that AD bisects ∠BAC then:
(a) BD = CD
(b) CD > CA
(c) BD > BA
(d) BA > BD
Answer : (d) BA > BDShow Answer :
Question : If ABC is an equilateral triangle, then each angle equals to:
(a) 90°
(b)180°
(c) 120°
(d) 60°
Answer :(d) 60°Show Answer :
Question : D is a point on the side BC of a ΔABC such that AD bisects ∠BAC. Then
(a) BD = CD
(b) BA > BD
(c) BD > BA
(d) CD > CA
Answer :(b) BA > BDShow Answer :
Question : It is not possible to construct a triangle when the lengths of its sides are
(a) 4 cm, 6 cm, 6 cm
(b) 9.3 cm, 5.2 cm, 7.4 cm
(c) 6 cm, 7 cm, 8 cm
(d) 5.3 cm, 2.2 cm, 3.1 cm
Answer :(d) 5.3 cm, 2.2 cm, 3.1 cmShow Answer :
Question : If ΔABC ≌ ΔPQR then which of the following is true:
(a) CA = RP
(b) AB = RP
(c) AC = RQ
(d) CB = QP
Answer :(a) CA = RPShow Answer :
Question : If two triangles ABC and PQR are congruent under the correspondence A ↔ P, B ↔ Q, and C ↔ R, then symbolically, it is expressed as
(a) ΔABC ≅ ΔPQR
(b) ΔABC = ΔPQR
(c) ΔABC and ΔPQR are scalene triangles
(d) ΔABC and ΔPQR are isosceles triangles
Answer :(a) ΔABC ≅ ΔPQRShow Answer :
Question : If AD is an altitude of an isosceles triangle ABC in which AB = AC. Then:
(a) BD=CD
(b) BD>CD
(c) BD<CD
(d) None of the above
Answer :((iii)Show Answer :
Question :If ΔABC ≅ ΔPQR then which of the following is true:
(a) CA = RP
(b) AB = RP
(c) AC = RQ
(d) CB = QP
Answer : (a) CA = RPShow Answer :
Question :If two triangles ABC and PQR are congruent under the correspondence A ↔ P, B ↔ Q, and C ↔ R, then symbolically, it is expressed as
(a) ΔABC ≅ ΔPQR
(b) ΔABC = ΔPQR
(c) ΔABC and ΔPQR are scalene triangles
(d) ΔABC and ΔPQR are isosceles triangles
Answer : (a) ΔABC ≅ ΔPQRShow Answer :
Question :If the bisector of the angle A of an △ABC is perpendicular to the base BC of the triangle then the triangle ABC is :
(a) Obtuse Angled
(b) Isosceles
(c) Scalene
(d) Equilateral
Answer : (b) IsoscelesShow Answer :
Question :If AB = QR, BC=RP and CA = QP, then which of the following holds?
(a) △BCA ≅ △PQR
(b) △ABC ≅ △PQR
(c) △CBA ≅ △PQR
(d) △CAB ≅ △PQR
Answer : (d) △CAB ≅ △PQRShow Answer :
Question :ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively. Then:
(a) BE > CF
(b) BE < CF
(c) BE = CF
(d) None of the above
Answer : (c) BE = CFShow Answer :
Question :Which of the following is not a criterion for congruence of triangles?
(a) SSS
(b) SSA
(c) ASA
(d) SAS
Answer : (b) SSAShow Answer :
Question :In a right triangle, the longest side is:
(a) Perpendicular
(b) Hypotenuse
(c) Base
(d) None of the above
Answer : (b) HypotenuseShow Answer :
Question :In △ABC, if ∠A = 45° and ∠B = 70°, then the shortest and the longest sides of the triangle are respectively,
(a) BC,AB
(a) AB,AC
(c) AB,BC
(d) BC,AC
Answer : (d) BC,ACShow Answer :
Question :If the altitudes from vertices of a triangle to the opposite sides are equal, then the triangles is
(a) Scalene
(b) Isosceles
(c) Equilateral
(d) Right-angled
Answer : (b) IsoscelesShow Answer :
Question :If ABC is an equilateral triangle, then each angle equals to:
(a) 90°
(b)180°
(c) 120°
(d) 60°
Answer : (d) 60°Show Answer :
Question :ABC ≅ △PQR. If AB=5 cm, and then which of the following is true?
(a) QR = 5 CM, ∠R= 60°
(b) QP = 5 cm, ∠P= 60°
(c) QP = 5cm, ∠R = 60°
(d) QR = 5 CM, ∠Q = 60°
Answer : (b) QP = 5 cm, ∠P= 60°Show Answer :
Question :O is any point in the interior of △ABC.Then which of the following is true?
(a) (OA+OB+OC) <
(b) (OA+OB+OC) > (AB+BC+CA)
(c) (OA+OB+OC) >
(d) None of the Above
Answer : (c) (OA+OB+OC) > Show Answer :
Question :It is not possible to construct a triangle when its sides are:
(a) 6 cm, 7 cm, 7 cm
(b) 5.4 cm, 2.3 cm, 3 cm
(c) 8.3 cm, 3.4 cm, 6.1 cm
(d) 3 cm, 5 cm, 5 cm
Answer : (b) 5.4 cm, 2.3 cm, 3 cmShow Answer :
Question :Two equilateral triangles are congruent when:
(a) Their areas are proportional
(b) Their sides are equal
(c) Their sides are proportional
(d) Their angles are equal
Answer : (b) Their sides are equalShow Answer :
Question :It is not possible to construct a triangle when the lengths of its sides are
(a) 4 cm, 6 cm, 6 cm
(b) 9.3 cm, 5.2 cm, 7.4 cm
(c) 6 cm, 7 cm, 8 cm
(d) 5.3 cm, 2.2 cm, 3.1 cm
Answer : (d) 5.3 cm, 2.2 cm, 3.1 cmShow Answer :
Question :Which of the following statements is incorrect?
(a) Two squares having the same side length are congruent
(b) Two rectangles having the same area are congruent
(c) Two circles having the same radius are congruent
(d) Two lines having same length are congruent
Answer : (b) Two rectangles having the same area are congruentShow Answer :
Question :ABCD is a parallelogram, if the two diagonals are equal, then by what criterion are the triangles ABD and ABC congruent
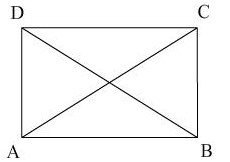
(a) AAS
(b) SSS
(c) SAS
(d) RHS
Answer : (b) SSSShow Answer :
Question : In a right triangle, the longest side is:
(a) Perpendicular
(b) Hypotenuse
(c) Base
(d) None of the above
Answer :(b) HypotenuseShow Answer :
Question : If ABC and DBC are two isosceles triangles on the same base BC. Then:
(a) ∠ABD = ∠ACD
(b) ∠ABD > ∠ACD
(c) ∠ABD < ∠ACD
(d) None of the above
Answer :(a) ∠ABD = ∠ACDShow Answer :
Question : In ΔABC, ∠C = ∠A and BC = 4 cm and AC = 5 cm, then find length of AB.
(a) 5 cm
(b) 3 cm
(c) 4 cm
(d) 2.5 cm
Answer :(c) 4 cmShow Answer :
Question : If AB = QR, BC=RP and CA = QP, then which of the following holds?
(a) △BCA ≅ △PQR
(b) △ABC ≅ △PQR
(c) △CBA ≅ △PQR
(d) △CAB ≅ △PQR
Answer :(d) △CAB ≅ △PQRShow Answer :
Question : If two sides of a triangle are equal, the angles opposite to these sides are
(a) supplementary
(b) equal
(c) right angles
(d) not equal
Answer :(b) equalShow Answer :
Question : In triangle ABC, if AB=BC and ∠B = 70°, ∠A will be:
(a) 70°
(b) 110°
(c) 55°
(d) 130°
Answer : cShow Answer :
Explanation: Given,
AB = BC
Hence, ∠A=∠C
And ∠B = 70°
By angle sum property of triangle we know:
∠A+∠B+∠C = 180°
2∠A+∠B=180°
2∠A = 180-∠B = 180-70 = 110°
∠A = 55°
Question : For two triangles, if two angles and the included side of one triangle are equal to two angles and the included side of another triangle. Then the congruency rule is:
(a) SSS
(b) ASA
(c) SAS
(d) None of the above
Answer : bShow Answer :
Question : A triangle in which two sides are equal is called:
(a) Scalene triangle
(b) Equilateral triangle
(c) Isosceles triangle
(d) None of the above
Answer : cShow Answer :
Question : Which of the following is not a criterion for congruence of triangles?
(a) SAS
(b) ASA
(c) SSA
(d) SSS
Answer :cShow Answer :
Explanation:
SSA is not a criterion for the congruence of triangles. Whereas SAS, ASA and SSS are the criteria for the congruence of triangles.
Question : In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are
(a) Isosceles and congruent
(b) Isosceles but not congruent
(c) Congruent but not isosceles
(d) Neither congruent nor isosceles
Answer :bShow Answer :
Explanation:
Consider two triangles, ABC and PQR. If the sides AB = AC and ∠C = ∠P and ∠B = ∠Q, then the two triangles are said to be isosceles, but they are not congruent.
Question : In ∆ PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is
(a) 2 cm
(b) 2.5 cm
(c) 4 cm
(d) 5 cm
Answer :cShow Answer :
Explanation:
Given that, in a triangle PQR, ∠R = ∠P.
Since, ∠R = ∠P, the sides opposite to the equal angles are also equal.
Hence, the length of PQ is 4 cm.
Question : If AB = QR, BC = PR and CA = PQ, then
(a) ∆ PQR ≅ ∆ BCA
(b) ∆ BAC ≅ ∆ RPQ
(c) ∆ CBA ≅ ∆ PRQ
(d) ∆ ABC ≅ ∆ PQR
Answer :cShow Answer :
Explanation:
Consider two triangles ABC and PQR.
Given that, AB = QR, BC = PR and CA = PQ.
By using Side-Side-Side (SSS rule),
We can say, ∆ CBA ≅ ∆ PRQ.
Question : If ∆ ABC ≅ ∆ PQR, then which of the following is not true?
(a) AC = PR
(b) BC = PQ
(c) QR = BC
(d) AB = PQ
Answer :bShow Answer :
Explanation:
Given that, ∆ ABC ≅ ∆ PQR
Hence, AB = PQ
BC = QR
AC =PR
Thus, BC = PQ is not true, if ∆ ABC ≅ ∆ PQR.
Question : In ∆ ABC, BC = AB and ∠B = 80°. Then ∠A is equal to
(a) 40°
(b) 50°
(c) 80°
(d) 100°
Answer :b Show Answer :
Explanation: In a triangle, ABC, BC = AB and ∠B = 80°.
Thus, the given triangle is an isosceles triangle.
By using the angle sum property of a triangle, we get
x + 80°+ x = 180°
2x + 80°= 180°
2x = 180°- 80°
2x = 100°
x = 100°/2 = 50°
Therefore, ∠A = 50°.
Question : Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be
(a) 3.4 cm
(b) 3.6 cm
(c) 3.8 cm
(d) 4.1 cm
Answer :aShow Answer :
Explanation: If two sides of a triangle are of lengths 5 cm and 1.5 cm, then the length of the third side of the triangle cannot be 3.4 cm. Because the difference between the two sides of a triangle should be less than the third side.
Question : In ∆ ABC, AB = AC and ∠B = 50°. Then ∠C is equal to
(a) 40°
(b) 50°
(c) 80°
(d) 130°
Answer :bShow Answer :
Explanation:
Given that, in a triangle ABC, AB = AC and ∠B = 50°.
Since the given triangle is an isosceles triangle, the angles opposite to the equal sides are also equal. Hence, ∠C = 50°.
Question : In ∆ PQR, if ∠R > ∠Q, then
(a) QR < PR
(b) PQ < PR
(c) PQ > PR
(d) QR > PR
Answer :cShow Answer :
Explanation: In a triangle PQR, if ∠R > ∠Q, then PQ > PR, because the side opposite to the greater angle is longer.
Question : It is given that ∆ ABC ≅ ∆ FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
(a) DF = 5 cm, ∠F = 60°
(b) DF = 5 cm, ∠E = 60°
(c) DE = 5 cm, ∠E = 60°
(d) DE = 5 cm, ∠D = 40
Answer :bShow Answer :
Explanation:
Given that, ∆ ABC ≅ ∆ FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°.
By using the CPCT rule,
DF = 5 cm, since AB = 5 cm.
Again by using the CPCT rule, ∠E = ∠C.
Therefore, ∠E = ∠C = 180° – (∠A+ ∠B) [ By using angle sum property of triangle]
∠E = 180° – (80°+ 40°)
∠E = 180° – 120°
∠E = 60°
Question : In the given figure, ΔABC ~ ΔDCB, then
AB × DB =
(a) OA × OD
(b) OB × OC
(c) AB × DC
(d) DC × AC
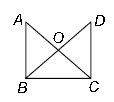
Answer 😀Show Answer :
Question : In the given trapezium ABCD, AB||CD and AB = 2CD. If area of ΔAOB = 84 cm2, then the area of ΔCOD is
(a) 22 sq.cm
(b) 25 sq.cm
(c) 21 sq.cm
(d) 24 sq.cm
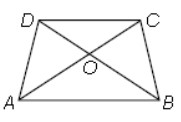
Answer :CShow Answer :
Question : If a tree casts a 18 feet shadow and at the same time, a child of height 3 feet casts a 2 feet shadow, then the height of the tree is
(a) 27 feet
(b) 32 feet
(c) 45 feet
(d) 36 feet
Answer :AShow Answer :
Question : Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, then the distance between their tops is
(a) 13 m
(b) 12 m
(c) 14 m
(d) 15 m
Answer :AShow Answer :
Question : A 12 cm rod is held between a flashlight and a wall as shown. Find the length of the shadow on the wall if the rod is 45 cm from the wall and 15 cm from the light.
(a) 75 cm
(b) 96 cm
(c) 48 cm
(d) 60 cm
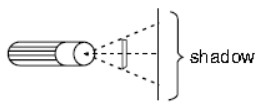
Answer :CShow Answer :
Question : An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1/2X1 hours?
(a) 300 √67 km
(b) 400 √61 km
(c) 200 √61 km
(d) 300 √61 km
Answer 😀Show Answer :
Question : Mason Construction wants to connect two parks on opposite sides of town with a road. Surveyors have laid out a map as shown. The road can be built through the town or around town through point R. The roads intersect at a right angle at point R. The line joining Park A to Park B is parallel to the line joining C and D.
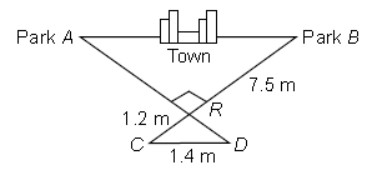
(a) What is the distance between the parks through town?
(b) What is the distance from Park A to Park B through point R?
(i) (ii)
(a) 9 m 13 m
(b) 8 m 12.5 m
(c) 8.75 m 12 m
(d) 9 m 14 m
Answer :CShow Answer :
Question : In rhombus ABCD, AB2 + BC2 + CD2 + DA2 =
(a) OA2 + OB2
(b) OB2 + OC2
(c) OC2 + OD2
(d) AC2 + BD2
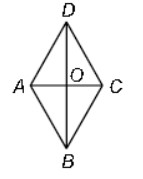
Answer 😀Show Answer :
Question : In the given figure, ∠BAC = ∠ADC, then CA/CB is
(a) CB × CD
(b) CA2
(c) DC/AC
(d) CD2
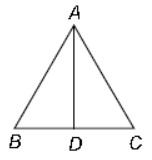
Answer :CShow Answer :
Question : P and Q are points on sides AB and AC respectively of DABC. If AP = 3 cm, PB = 6 cm, AQ = 5 cm and QC = 10 cm, then BC =
(a) PQ
(b) 2PQ
(c) 3PQ
(d) 4PQ
Answer :CShow Answer :
Question : In the given figure, AD ⊥ BC, BE ⊥ AC, CF ⊥ AB, then AF2 + BD2 + CE2 =
(a) OA2 + OB2 + OC2
(b) OD2 + OE2 + OF2
(c) AB2 + BC2 + AC2
(d) AE2 + BF2 + CD2
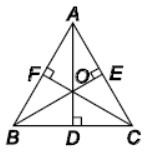
Answer 😀Show Answer :
Question :ABC is right triangle, right angled at C. If p is the length of the perpendicular from C to AB and a, b, c have the usual meaning, then 1/a2 + 1/b2
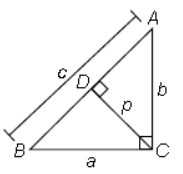
(A) 1/p2
(b) 2/p2
(c) p2
(d) 2p2
Answer :AShow Answer :
Question : In the given ΔABC, AD ⊥ BC and ∠A is right angled. Then AD2 =
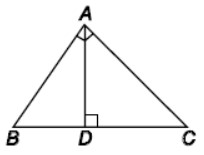
(A) AB × AC
(b) BD × CD
(c) BC × AC
(d) AB × BC
Answer :BShow Answer :
Question : ΔABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ΔDEF ~ ΔABC and EF = 4 cm, then perimeter of ΔDEF is
(a) 7.5 cm
(b) 15 cm
(c) 22.5 cm
(d) 30 cm
Answer :BShow Answer :
Question : In the given figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm, AD = 4 cm, then CD =
(a) 16 cm
(b) 14 cm
(c) 15 cm
(d) 17 cm
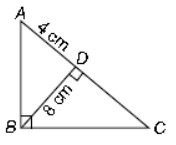
Answer :AShow Answer :
Question : In the given figure, ABC is a right triangle right-angled at B. AD and CE are the two medians drawn from A and C respectively. If AC = 5 cm and AD = 3 √5 / 2 cm, then the length of CE is
(a) 4 cm A
(b) 2 5cm
(c) 3 5cm
(d) 5 cm
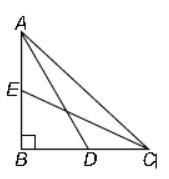
Answer :BShow Answer :
Question : Match the following

(A) (P)→(1), (Q)→(2), (R)→(3), (S)→(4)
(b) (P)→(2), (Q)→(1), (R)→(3), (S)→(4)
(c) (P)→(4), (Q)→(2), (R)→(1), (S)→(3)
(d) (P)→(3), (Q)→(1), (R)→(4), (S)→(2)
Answer :BShow Answer :
Question : Which of the following statements is CORRECT?
(a) The ratio of the areas of two similar triangles is equal to the ratio of their corresponding sides.
(b) If a line is drawn parallel to one side of the triangle to intersect the other two sides in distinct points then the other two sides are divided in the same ratio.
(c) All similar figures are congruent.
(d) If in two triangles, two angles of one triangle is equal to the two angles of the other triangle then two triangles may or may not be congruent.
Answer :BShow Answer :
Question :P and Q are the mid-points of the sides CA and CB respectively of a ΔABC, right angled at C, then find :
(i) 4AC2 + BC2
(b) 4BC2 + AC2
(c) 4(AQ2 + BP2)
(i) (ii) (iii)
(a) 4AQ2 4BP2 5AB2
(b) 5AQ2 5BP2 4AB2
(c) 4AQ2 5BP2 5AB2
(d) 5AQ2 4BP2 4AB2
Answer :AShow Answer :
Question : In the given figure, the line segment XY is parallel to side AC of ΔABC and it divides the triangle into two parts of equal area. Then, find
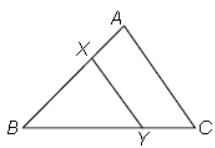
(i) AX : AB (ii) AC/XY(i) (ii)
(A) (2 + √2): 2 √2 − 2
(b) (2 − √2): 2 √2 −1
(c) (2 − √3): 3 3
(d) (2 + √2): 3 √2 − 3
Answer :BShow Answer :
Question : The angles opposite to equal sides of a triangle are:
(a) Equal
(b) Unequal
(c) supplementary angles
(d) Complementary angles
Answer : aShow Answer :
Question : If E and F are the midpoints of equal sides AB and AC of a triangle ABC. Then:
(a) BF = AC
(b) BF = AF
(c) CE = AB
(d) BF = CE
Answer : dShow Answer :
Explanation: AB and AC are equal sides.
AB = AC (Given)
∠A = ∠A (Common angle)
AE = AF (Halves of equal sides)
∆ ABF ≅ ∆ ACE (By SAS rule)
Hence, BF = CE (CPCT)
Question : ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB, respectively. Then:
(a) BE > CF
(b) BE < CF
(c) BE = CF
(d) None of the above
Answer : cShow Answer :
Explanation:
∠A = ∠A (common arm)
∠AEB = ∠AFC (Right angles)
AB = AC (Given)
∴ ΔAEB ≅ ΔAFC
Hence, BE = CF (by CPCT)
Question : If ABC and DBC are two isosceles triangles on the same base BC. Then:
(a) ∠ABD = ∠ACD
(b) ∠ABD > ∠ACD
(c) ∠ABD < ∠ACD
(d) None of the above
Answer : aShow Answer :
Explanation: AD = AD (Common arm)
AB = AC (Sides of isosceles triangle)
BD = CD (Sides of isosceles triangle)
So, ΔABD ≅ ΔACD.
∴ ∠ABD = ∠ACD (By CPCT)
Question : If the altitudes from vertices of a triangle to the opposite sides are equal, then the triangles is
(a) Scalene
(b) Isosceles
(c) Equilateral
(d) Right-angled
Answer :(b) IsoscelesShow Answer :
Question : In ΔPQR, if ∠R > ∠Q, then
(a) QR > PR
(b) PQ > PR
(c) PQ < PR
(d) QR < PR
Answer :(b) PQ > PRShow Answer :
Question : In △ABC, if ∠A = 45∘ and ∠B = 70∘, then the shortest and the longest sides of the triangle are respectively,
(a) BC,AB
(i) AB,AC
(c) AB,BC
(d) BC,AC
Answer :(d) BC,ACShow Answer :
Question : The perimeter of a triangle is _ the sum of its medians.
(a) less than
(b) greater than twice
(c) equal to
(d) greater than
Answer :(d) greater thanShow Answer :
Question : ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively. Then:
(a) BE > CF
(b) BE < CF
(c) BE = CF
(d) None of the above
Answer :(c) BE = CFShow Answer :
Question : In a right triangle, the longest side is:
(a) Perpendicular
(b) Hypotenuse
(c) Base
(d) None of the above
Answer :(b) HypotenuseShow Answer :
Question :In △ABC, if ∠B = 30° and ∠C = 70°, then which of the following is the longest side?
(a) AB
(b) BC
(c) AC
(d) AB or AC
Answer : (b) BCShow Answer :
Question :The angles opposite to equal sides of a triangle are:
(a) Equal
(b) Unequal
(c) supplementary angles
(d) Complementary angles
Answer : (a) EqualShow Answer :
Question :△ABC = △PQR, then which of the following is true?
(a) CB = QP
(b) CA = RP
(c) AC = RQ
(d) AB = RP
Answer : (b) CA = RPShow Answer :
Question :In △ABC and △DEF, AB = DE and ∠A = ∠D.Then two triangles will be congruent by SA axiom if:
(a) BC = EF
(b) AC = EF
(c) AC = DE
(d) BC = DE
Answer : (c) AC = DEShow Answer :
Question : △ABC = △PQR, then which of the following is true?
(a) CB = QP
(b) CA = RP
(c) AC = RQ
(d) AB = RP
Answer :(b) CA = RPShow Answer :
Question : A triangle can have:
(a) Two obtuse angles
(b) Two acute angles
(c) Two right angles
(d) All angles more than 60°
Answer :(b) Two acute anglesShow Answer :
Question : The angles opposite to equal sides of a triangle are:
(a) Equal
(b) Unequal
(c) supplementary angles
(d) Complementary angles
Answer :(a) EqualShow Answer :
Question : In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to:
(a) 80°
(b) 40°
(c) 50°
(d) 100°
Answer :(c) 50°Show Answer :
Question : In △ABC, ∠A = 35∘ and ∠B = 65∘, then the longest side of the triangle is:
(a) AC
(b) BC
(c) AB
(d) None of these
Answer :(c) ABShow Answer :
Question : If ABC is an equilateral triangle, then each angle equals to:
(a) 90°
(b)180°
(c) 120°
(d) 60°
Answer : dShow Answer :
Explanation: Equilateral triangle has all its sides equal and each angle measures 60°.
AB= BC = AC (All sides are equal)
Hence, ∠A = ∠B = ∠C (Opposite angles of equal sides)
Also, we know that,
∠A + ∠B + ∠C = 180°
⇒ 3∠A = 180°
⇒ ∠A = 60°
∴ ∠A = ∠B = ∠C = 60°
Question : If AD is an altitude of an isosceles triangle ABC in which AB = AC. Then:
(a) BD = CD
(b) BD > CD
(c) BD < CD
(d) None of the above
Answer : aShow Answer :
Explanation: In ΔABD and ΔACD,
∠ADB = ∠ADC = 90°
AB = AC (Given)
AD = AD (Common)
∴ ΔABD ≅ ΔACD (By RHS congruence condition)
BD = CD (By CPCT)
Question : In a right triangle, the longest side is:
(a) Perpendicular
(b) Hypotenuse
(c) Base
(d) None of the above
Answer : bShow Answer :
Explanation: In triangle ABC, right-angled at B.
∠B = 90
By angle sum property, we know:
∠A + ∠B + ∠C = 180
Hence, ∠A + ∠C = 90
So, ∠B is the largest angle.
Therefore, the side (hypotenuse) opposite to the largest angle will be the longest one.



