Class 9 Mathematics MCQ Heron’s Formula

Class 9 Mathematics MCQ Heron’s Formula with Answers is Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 9 Mathematics MCQ Heron’s Formula with Answers to know their preparation level.

Students who are searching for NCERT Class 9 Mathematics MCQ Heron’s Formula with Answers are compiled here to get good practice on all fundamentals. Know your preparation level on MCQ Questions for Class 9 Mathematics MCQ Heron’s Formula with Answers. You can also verify your answers from the provided Class 9 Mathematics MCQ Heron’s Formula with Answers. So, ace up your preparation with MCQ of Class 9 Mathematics MCQ & NCERT Textbook solutions Examinations.

NCERT Class 9 Mathematics MCQ Heron’s Formula with Answers

Question :Each side of an equilateral triangle measures 10 cm. Then the area of the triangle is
(a) 43.3 cm²
(b) 43.1 cm²
(c) 43.4 cm²
(d) 43.2 cm²

Show Answer :

Answer : (a) 43.3 cm²

Question :The length of the sides of a triangle are 5 cm, 7 cm and 8 cm. Area of the triangle is :
(a) 10√3 cm²
(b) 100√3 cm²
(c) 300 cm²
(d) 50√3 cm²

Show Answer :

Answer : (a) 10√3 cm²

Question :The area of a triangle with base 8 cm and height 10 cm is
(a) 20 cm²
(b) 18 cm²
(c) 80 cm²
(d) 40 cm²

Show Answer :

Answer : (d) 40 cm²

Question :Find the length of each side of an equilateral triangle having area of 9 root 3 cm square
(a) 36 cm
(b) 5 cm
(c) 15 cm
(d) 6 cm

Show Answer :

Answer : (d) 6 cm

Question : If the height of a parallelogram having 500 cm2 as the area is 20 cm, then its base is of length
(a) 25 cm
(b) 15 cm
(c) 20 cm
(d) 50 cm

Show Answer :

Answer :(a) 25 cm

Question : The area of triangle with given two sides 18cm and 10cm respectively and perimeter equal to 42 cm is:
(a) 20√11 cm²
(b) 19√11 cm²
(c) 22√11 cm²
(d) 21√11 cm²

Show Answer :

Answer :(d) 21√11 cm²

Question : The perimeter of an equilateral triangle is 60 m. The area is
(a) 10√3 m²
(b) 15√3 m²
(c) 20√3 m²
(d) 100√3 m²

Show Answer :

Answer :(d) 100√3 m²

Question : The area of a triangle with base 8 cm and height 10 cm is
(a) 20 cm²
(b) 18 cm²
(c) 80 cm²
(d) 40 cm²

Show Answer :

Answer :(d) 40 cm²

Question : An isosceles right triangle has area 8 cm2. The length of its hypotenuse is :
(a) √16 cm
(b) √48 cm
(c) √32 cm
(d) √24 cm

Show Answer :

Answer :(c) √32 cm

Question : Ength of perpendicular drawn on smallest side of scalene triangle is
(a) Smallest
(b) Largest
(c) No relation
(d) None

Show Answer :

Answer :(c) No relation

Question : The area of an equilateral triangle having side length equal to √3/4cm is:
(a) 2/27 cm²
(b) 2/15 cm²
(c) 3/16 cm²
(d) 3/14 cm²

Show Answer :

Answer :(c) 3/16 cm²

Question :The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 70 paise per cm² is
(a) ₹17
(b) ₹16.80
(c) ₹7
(d) ₹16

Show Answer :

Answer : (b) ₹16.80

Question :The lengths of a triangle are 6 cm, 8 cm and 10 cm. Then the length of perpendicular from the opposite vertex to the side whose length is 8cm is:
(a) 4 cm
(b) 6 cm
(c) 5 cm
(d) 2 cm

Show Answer :

Answer : (b) 6 cm

Question :The area of an equilateral triangle having side length equal to $\frac { \sqrt { 3 } }{ 4 }$ cm is:
(a) $\frac { 2 }{ 27 }$ sq.cm
(b) $\frac { 2 }{ 15 }$ sq.cm
(c) $\frac { 3 }{ 16 }$ sq.cm
(d) $\frac { 3 }{ 14 }$ sq.cm

Show Answer :

Answer : (c) $\frac { 3 }{ 16 }$ sq.cm

Question :he base of an isosceles triangle is 10 cm and one of its equal sides is 13 cm. The area of the triangle is
(a) 80 cm²
(b) 100 cm²
(c) 50 cm²
(d) 60 cm²

Show Answer :

Answer : (d) 60 cm²

Question :The area of an equilateral triangle of side 6 cm is
(a) 18 cm²
(b) 9√3 cm²
(c) 56√3 cm²
(d) 58√3 cm²

Show Answer :

Answer : (b) 9√3 cm²

Question : The area of a triangle with given two sides 18 cm and 10 cm, respectively and a perimeter equal to 42 cm is:
(a) 20√11 cm²
(b) 19√11 cm²
(c) 22√11 cm²
(d) 21√11 cm²

Show Answer :

Answer : d
Explanation: Perimeter = 42
a + b + c = 42
18 + 10 + c = 42
c = 42 – 28 = 14 cm
Semi perimeter, s = 42/2 = 21 cm
Using Heron’s formula:

\begin{array}{l} A = \sqrt{s (s - a) (s - b) (s - c)} \end{array}

= √[21(21 – 18)(21 – 10)(21 – 14)]

= √(21 × 3 × 11 × 7)
= 21√11 cm²

Question : The sides of a triangle are in the ratio 12: 17: 25 and its perimeter is 540 cm. The area is:
(a) 1000 sq.cm
(b) 5000 sq.cm
(c) 9000 sq.cm
(d) 8000 sq.cm

Show Answer :

Answer : c
Explanation: The ratio of the sides is 12: 17: 25
Perimeter = 540 cm
Let the sides of the triangle be 12x, 17x and 25x.
Hence,
12x + 17x + 25x = 540 cm
54x = 540 cm
x = 10
Therefore,
a = 12x = 12 × 10 = 120
b = 17x = 17 × 10 = 170
c = 25x = 25 × 10 = 250
Semi-perimeter, s = 540/2 = 270 cm
Using Heron’s formula:

\begin{array}{l} A = \sqrt{s (s - a) (s - b) (s - c)} \end{array}

= √[270(270 – 120)(270 – 170)(270 – 250)]

= √(270 × 150 × 100 × 20)
= 9000 sq.cm

Question : The equal sides of the isosceles triangle are 12 cm, and the perimeter is 30 cm. The area of this triangle is:
(a) 9√15 sq.cm
(b) 6√15 sq.cm
(c) 3√15 sq.cm
(d) √15 sq.cm

Show Answer :

Answer : a
Explanation: Given,
Perimeter = 30 cm
Semiperimeter, s = 30/2 = 15 cm
a = b = 12 cm
c = ?
a + b + c = 30
12 + 12 + c = 30
c = 30 – 24 = 6 cm
Using Heron’s formula:

\begin{array}{l} A = \sqrt{s (s - a) (s - b) (s - c)} \end{array}

= √[15(15 – 12)(15 – 12)(15 – 6)]

= √(15 × 3 × 3 × 9)
= 9√15 sq.cm

Question : The sides of a triangle are 122 m, 22 m and 120 m respectively. The area of the triangle is:
(a) 1320 sq.m
(b) 1300 sq.m
(c) 1400 sq.m
(d) 1420 sq.m

Show Answer :

Answer : a
Explanation: Given,
a = 122 m
b = 22 m
c = 120 m
Semi-perimeter, s = (122 + 22 + 120)/2 = 132 m
Using heron’s formula:

\begin{array}{l} A = \sqrt{s (s - a) (s - b) (s - c)} \end{array}

= √[132(132 – 122)(132 – 22)(132 – 120)]

= √(132 × 10 × 110 × 12)
= 1320 sq.m

Question : A quadrilateral whose sides are 3 cm, 4 cm, 4 cm, 5 cm and one of the diagonal is equal to 5 cm as per the below figure. The area of the quadrilateral is:

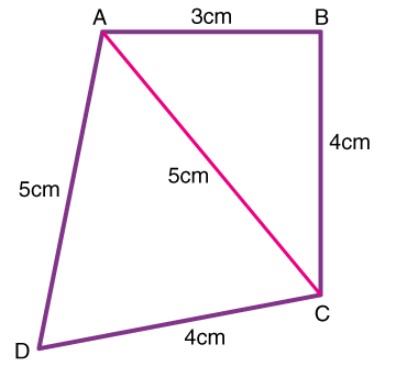
(a) 19.17 sq.cm
(b) 15.17 sq.cm
(c) 20.17 sq.cm
(d) 22.17 sq.cm.

Show Answer :

Answer : b
Explanation: Using Pythagoras theorem, in ΔABC,
AC² = AB² + BC²
⇒ 5² = 3² + 4²
⇒ 25 = 25
Hence, ABC is a right triangle.
Area of ΔABC = ½ x 3 x 4 = 6 sq.cm
Semiperimeter of ΔACD = s = (5+5+4)/2 = 14/2 = 7 cm
Area of ΔACD can be determined by using Heron’s formula.

\begin{array}{l} A = \sqrt{s (s - a) (s - b) (s - c)} \end{array}

= √[7(7 – 5)(7 – 5)(7 – 4)]

= √(7 × 2 × 2 × 3)
= 9.17 sq.cm
Therefore, the area of quad.ABCD = Area of ΔABC + Area of ΔACD = (6 + 9.17) sq.cm = 15.17 sq.cm

Question : The area of an equilateral triangle having side length equal to √3/4 cm (using Heron’s formula) is:
(a) 2/27 sq.cm
(b) 2/15 sq.cm
(c) 3√3/64 sq.cm
(d) 3/14 sq.cm

Show Answer :

Answer : c
Explanation: Here, a = b = c = √3/4
Semiperimeter = (a + b + c)/2 = 3a/2 = 3√3/8 cm
Using Heron’s formula,

\begin{array}{l} A = \sqrt{s (s - a) (s - b) (s - c)} \end{array}

= √[(3√3/8) (3√3/8 – √3/4)(3√3/8 – √3/4)(3√3/8 – √3/4)]

= 3√3/64 sq.cm

Question : The sides of a parallelogram are 100 m each and the length of the longest diagonal is 160 m. The area of a parallelogram is:
(a) 9600 sq.m
(b) 9000 sq.m
(c) 9200 sq.m
(d) 8800 sq.m

Show Answer :

Answer : a
Explanation: The diagonal divides the parallelogram into two equivalent triangles. Hence, its area will be equal to the sum of the area of the two triangles.
Thus, the sides of one triangle will be 100 m, 160 m, and 100 m.
So, a = 100 m, b = 160 m, c = 100 m
Semiperimeter (s) = (a + b + c)/2 = (100 + 160 + 100)/2 = 360/2 = 180 m
Using Heron’s formula,

\begin{array}{l} A = \sqrt{s (s - a) (s - b) (s - c)} \end{array}

= √[180(180 – 100)(180 – 160)(180 – 100)]

= √(180 × 80 × 20 × 80)
= 4800 sq.m
Thus, the area of the parallelogram = 2 × 4800 sq.m = 9600 sq.m

Question : The sides of a triangle are in the ratio of 3: 5: 7 and its perimeter is 300 cm. Its area will be:
(a) 1000√3 sq.cm
(b) 1500√3 sq.cm
(c) 1700√3 sq.cm
(d) 1900√3 sq.cm

Show Answer :

Answer : b
Explanation:
The ratio of the sides is 3: 5: 7
Perimeter = 300 cm
Let the sides of the triangle be 3x, 5x and 7x.
Hence,
3x + 5x + 7x = 300 cm
15x = 300 cm
x = 20
Therefore,
a = 3x = 3 × 20 = 60
b = 5x = 5 × 20 = 100
c = 7x = 7 × 20 = 140
Semi-perimeter, s = 300/2 = 150 cm
Using Heron’s formula:

\begin{array}{l} A = \sqrt{s (s - a) (s - b) (s - c)} \end{array}

= √[150(150 – 60)(150 – 100)(150 – 140)]

= √(150 × 90 × 50 × 10)
= 1500√3 sq.cm

Question : The base of a right triangle is 8 cm and the hypotenuse is 10 cm. Its area will be
(a) 24 cm²
(b) 40 cm²
(c) 48 cm²
(d) 80 cm²

Show Answer :

Answer :a
Explanation:
Given: Base = 8 cm and Hypotenuse = 10 cm
Hence, height = √[(10² – 8²) = √36 = 6 cm
Therefore, area = (½)×b×h = (½)×8×6 = 24 cm².

Question : The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm² is
(a) Rs 2.00
(b) Rs 2.16
(c) Rs 2.48
(d) Rs 3.00

Show Answer :

Answer :b
Explanation:
Given: a = 6 cm, b = 8 cm, c = 10 cm.
s = (6 + 8 + 10)/2 = 12 cm
Hence, by using Heron’s formula, we can write:
A = √[12(12 – 6)(12 – 8)(12 – 10)] = √[(12)(6)(4)(2)] = √576 = 24 cm²
Therefore, the cost of painting at a rate of 9 paise per cm² = 24 × 9 paise = Rs. 2.16

Question : An isosceles right triangle has an area of 8 cm². The length of its hypotenuse is
(a) √32 cm
(b) √16 cm
(c) √48 cm
(d) √24 cm

Show Answer :

Answer : a
Explanation:
Given that area of the isosceles triangle = 8 cm².
As the given triangle is isosceles triangle, let base = height = h
Hence,
(½)×h×h = 8
(½)h² = 8
h²= 16
h = 4 cm
Since it is isosceles right triangle, Hypotenuse² = Base²+Height²
Hypotenuse²= 4²+ 4²
Hypotenuse² = 32
Hypotenuse = √32 cm

Question : The area of an isosceles triangle having a base 2 cm and the length of one of the equal sides 4 cm, is
(a) √15 cm²
(b) √(15/2) cm²
(c) 2√15 cm²
(d) 4√15 cm²

Show Answer :

Answer :a
Explanation:
Given that a = 2 cm, b= c = 4 cm
s = (2 + 4 + 4)/2 = 10/2 = 5 cm
By using Heron’s formula, we get:
A =√[5(5 – 2)(5 – 4)(5 – 4)] = √[(5)(3)(1)(1)] = √15 cm².

Question : The perimeter of an equilateral triangle is 60 m. The area is
(a) 10√3 m²
(b) 15√3 m²
(c) 20√3 m²
(d) 100√3 m²

Show Answer :

Answer :d
Explanation:
Given: Perimeter of an equilateral triangle = 60 m
3a = 60 m (As the perimeter of an equilateral triangle is 3a units)
a = 20 cm.
We know that area of equilateral triangle = (√3/4)a² square units
A = (√3/4)20²
A = (√3/4)(400) = 100√3 m².

Question : The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude
(a) 16√5 cm
(b) 10√5 cm
(c) 24√5 cm
(d) 28 cm

Show Answer :

Answer :c
Explanation:
Given: a = 35 cm, b = 54cm, c = 61cm
s = (35 + 54 + 61)/2 = 150/2 = 75 cm.
Hence, by using Heron’s formula, A = √[75(75 – 35)(75 – 54)(75 – 61)] = √(882000) = 420√5 cm²
The area of triangle with longest altitude “h” is given as”
(½)×a×h = 420√5 {a is less than b and c}
(½)×35×h = 420√5
h = (840√5)/35 = 24√5 cm.

Question : The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is
(a) 1322 cm²
(b) 1311 cm²
(c) 1344 cm²
(d) 1392 cm²

Show Answer :

Answer :c
Explanation:
Since, all the sides of a triangle are given, we can find the area of a triangle using Heron’s formula.
Let a = 56 cm, b= 60 cm, c = 52 cm
s = (56+60+52)/2 = 84 cm.
Area of triangle using Heron’s formula, A = √[s(s-a)(s-b)(s-c)] square units
A = √[84(84-56)(84-60)(84-52)] = √(1806336) =1344 cm².

Question : If the area of an equilateral triangle is 16√3 cm², then the perimeter of the triangle is
(a) 48 cm
(b) 24 cm
(c) 12 cm
(d) 36 cm

Show Answer :

Answer :b
Explanation:
Given: Area of equilateral triangle = 16√3 cm²
(√3/4)a² = 16√3
a² = [(16√3)(4)]/√3
a² = 64
a = 8cm
Therefore, perimeter = 3(8) = 24 cm.

Question : The area of an equilateral triangle with sides 2√3 cm is
(a) 5.196 cm²
(b) 0.866 cm²
(c) 3.496 cm²
(d) 1.732 cm²

Show Answer :

Answer :a
Explanation:
Given: Side = 2√3 cm
We know that, area of equilateral triangle = (√3/4)a² square units
A = (√3/4)(2√3)² = (√3/4)(12) = 3√3 = 3(1.732) = 5.196 cm².

Question : The length of each side of an equilateral triangle having an area of 9√3 cm² is
(a) 8 cm
(b) 36 cm
(c) 4 cm
(d) 6 cm

Show Answer :

Answer :d
Explanation:
Given: Area of equilateral triangle = 9√3 cm²
Hence, (√3/4)a² = 9√3
a² = [(9√3)(4)]/√3
a² = 36
a = 6 cm.

Question :Length of perpendicular drawn on longest side of a scale △ is
(a) Smallest
(b) Largest
(c) No relation
(d) None

Show Answer :

Answer : (a) Smallest

Question :The perimeter of a rhombus is 20 cm. One of its diagonals is 8 cm. Then area of the rhombus is
(a) 24 cm²
(b) 42 cm²
(c) 18 cm²
(d) 36 cm²

Show Answer :

Answer : (a) 24 cm²

Question :If the height of a parallelogram having 500 cm² as the area is 20 cm, then its base is of length
(a) 25 cm
(b) 15 cm
(c) 20 cm
(d) 50 cm

Show Answer :

Answer : (a) 25 cm

Question :The area of quadrilateral PQRS, in which PQ = 7 cm, QR = 6 cm, RS = 12 cm, PS = 15 cm and PR = 9 cm:
(a) 74.98 cm²
(b) 25.25 cm²
(c) 75 cm²
(d) 68.25 cm²

Show Answer :

Answer : (a) 74.98 cm²

Question :The perimeter of a rhombus is 146 cm. One of its diagonals is 55 cm. The length of the other diagonal and area of the rhombus are
(a) 48 cm, 2320 cm²
(b) 48 cm, 1820 cm²
(c) 88 cm, 1320 cm²
(d) 48 cm, 1320 cm²

Show Answer :

Answer : (d) 48 cm, 1320 cm²

Question :ength of perpendicular drawn on smallest side of scalene triangle is
(a) Smallest
(b) Largest
(c) No relation
(d) None

Show Answer :

Answer : (c) No relation

Question :The area of a right angled triangle if the radius of its circumcircle is 3 cm and altitude drawn to the hypotenuse is 2 cm.
(a) 6 cm²
(b) 3 cm²
(c) 4 cm²
(d) 8 cm²

Show Answer :

Answer : (a) 6 cm²

Question :A square sheet whose perimeter is 32 cm is painted at the rate of Rs. 5 per m². The cost of painting is:
(a) ₹320
(b) ₹350
(c) ₹340
(d) ₹160

Show Answer :

Answer : (a) ₹320

Question :The area of a triangle whose sides are 12 cm, 16 cm and 20 cm is
(a) 96 cm²
(b) 320 cm²
(c) 240 cm²
(d) 72 cm²

Show Answer :

Answer : (a) 96 cm²

Question : The area of an equilateral triangle with side 2√3 cm is
(a) 5.196 cm²
(b) 0.866 cm²
(c) 3.496 cm²
(d) 1.732 cm²

Show Answer :

Answer :(a) 5.196 cm²

Question : The area of a right angled triangle if the radius of its circumcircle is 3 cm and altitude drawn to the hypotenuse is 2 cm.
(a) 6 cm²
(b) 3 cm²
(c) 4 cm²
(d) 8 cm²

Show Answer :

Answer :(a) 6 cm²

Question : The area of a right triangle of height 15 m and base 20 m is
(a) 160 m²
(b) 150 m²
(c) 210 m²
(d) 216 m²

Show Answer :

Answer :(b) 150 m²

Question : The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 70 paise per cm2 is
(a) ₹17
(b) ₹16.80
(c) ₹7
(d) ₹16

Show Answer :

Answer :(b) ₹16.80

Question : If the area of an equilateral triangle is 16√3 cm², then the perimeter of the triangle is
(a) 48 cm
(b) 24 cm
(c) 12 cm
(d) 36 cm

Show Answer :

Answer :(b) 24 cm

Question : A square sheet whose perimeter is 32 cm is painted at the rate of Rs. 5 per m2. The cost of painting is:
(a) ₹320
(b) ₹350
(c) ₹340
(d) ₹160

Show Answer :

Answer :(a) ₹320

Question : If side of a scalene △ is doubled then area would be increased by
(a) 100 %
(b) 50 %
(c) 25 %
(d) None of these

Show Answer :

Answer :(a) 100 %

Question : Each side of an equilateral triangle measures 10 cm. Then the area of the triangle is
(a) 43.3 cm²
(b) 43.1 cm²
(c) 43.4 cm²
(d) 43.2 cm²

Show Answer :

Answer :(a) 43.3 cm²

Question : The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm² is
(a) Rs 2.00
(b) Rs 2.16
(c) Rs 2.48
(d) Rs 3.00

Show Answer :

Answer :(b) Rs 2.16

Question : If the height of a parallelogram having 500 cm2 as the area is 20 cm, then its base is of length
(a) 25 cm
(b) 15 cm
(c) 20 cm
(d) 50 cm

Show Answer :

Answer :(a) 25 cm

Question : Semiperimeter of scalene triangle of side k, 2k and 3k is
(a) k
(b) 3k
(c) 4k
(d) 2k

Show Answer :

Answer :(b) 3k

Question : Area of a triangle is equal to:
(a) Base x Height
(b) 2(Base x Height)
(c) ½(Base x Height)
(d) ½ (Base + Height)

Show Answer :

Answer : c

Question : If the perimeter of an equilateral triangle is 180 cm. Then its area will be:
(a) 900 cm²
(b) 900√3 cm²
(c) 300√3 cm²
(d) 600√3 cm²

Show Answer :

Answer : b
Explanation: Given, Perimeter = 180 cm
3a = 180 (Equilateral triangle)
a = 60 cm
Semi-perimeter = 180/2 = 90 cm
Now as per Heron’s formula,

\begin{array}{l} A = \sqrt{s (s - a) (s - b) (s - c)} \end{array}

In the case of an equilateral triangle, a = b = c = 60 cm
Substituting these values in the Heron’s formula, we get the area of the triangle as:
A = √[90(90 – 60)(90 – 60)(90 – 60)]

= √(90× 30 × 30 × 30)
A = 900√3 cm²

CBSE Class 9 Mathematics MCQ Constructions with Answers

NCERT Solutions & Download NCERT Textbooks

Number System : Exercise – 1.1	Polynomials : Exercise – 2.1
Number System : Exercise – 1.2	Polynomials : Exercise – 2.2
Number System : Exercise – 1.3	Polynomials : Exercise – 2.3
Number System : Exercise – 1.4	Coordinate Geometry : Exercise – 3.1
Number System : Exercise – 1.5	Coordinate Geometry : Exercise – 3.2
Number System : Exercise – 1.6	Coordinate Geometry : Exercise – 3.3
Linear Equations in Two Variables : Exercise – 4.1	Introduction to Euclid’s Geometry : Exercise – 5.1
Linear Equations in Two Variables : Exercise – 4.2	Introduction to Euclid’s Geometry : Exercise – 5.2
Linear Equations in Two Variables : Exercise – 4.3	Introduction to Euclid’s Geometry : Exercise – 5.3
Linear Equations in Two Variables : Exercise – 4,4	Lines And Angles : Exercise – 6.1
Triangles : Exercise – 7.1	Lines And Angles : Exercise – 6.2
Triangles : Exercise – 7.2	Lines And Angles : Exercise – 6.3
Triangles : Exercise – 7.3	Quadrilaterals : Exercise – 8.1
Triangles : Exercise – 7.4	Areas of Parallelograms and Triangles : Exercise – 9.1
Triangles : Exercise – 7.5	Areas of Parallelograms and Triangles : Exercise – 9.2
Circles : Exercise – 10.1	Areas of Parallelograms and Triangles : Exercise – 9.3
Circles : Exercise – 10.2	Areas of Parallelograms and Triangles : Exercise – 9.4
Circles : Exercise – 10.3	Constructions : Exercise – 11.1
Circles : Exercise – 10.4	Constructions : Exercise – 11.2
Circles : Exercise – 10.5	Heron’s Formula : Exercise – 12.1
Circles : Exercise – 10.6	Heron’s Formula : Exercise – 12.2
Surface Areas and Volumes : Exercise – 13.1	Statistics : Exercise – 14.1
Surface Areas and Volumes : Exercise – 13.2	Statistics : Exercise – 14.2
Surface Areas and Volumes : Exercise – 13.3	Statistics : Exercise – 14.3
Surface Areas and Volumes : Exercise – 13.4	Statistics : Exercise – 14.4
Surface Areas and Volumes : Exercise – 13.5	Probability : Exercise – 15.1
Surface Areas and Volumes : Exercise – 13.6
Surface Areas and Volumes : Exercise – 13.7
Surface Areas and Volumes : Exercise – 13.8
Surface Areas and Volumes : Exercise – 13.9

Class 9 Mathematics MCQ Heron’s Formula

NCERT Class 9 Mathematics MCQ Heron’s Formula with Answers

CBSE Class 9 Mathematics MCQ Constructions with Answers

CBSE Class 9 Mathematics MCQ Circles with Answers

MCQ Questions Electrical Engineering Series Parallel Circuit

Leave a Reply Cancel reply

Class 9 Mathematics MCQ Heron’s Formula

NCERT Class 9 Mathematics MCQ Heron’s Formula with Answers

CBSE Class 9 Mathematics MCQ Constructions with Answers

CBSE Class 9 Mathematics MCQ Circles with Answers

MCQ Questions Electrical Engineering Series Parallel Circuit

Related Posts

Class 9 Mathematics MCQ

Class 9 Mathematics MCQ Lines And Angles

Leave a Reply Cancel reply