Multiple Choice Questions - Set - 1
Question 1:
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
(a) 60 cm²
(b) 65 cm²
(c) 30 cm²
(d) 32.5 cm²
Correct Answer – (A)
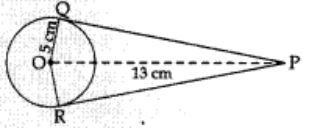
Reason: OP² = OQ² + PQ²
169 = 25 + PQ²
PQ² = 144
PQ = 12
Area PQOR = ar (AOPQ) + ar (AOPR)
= (1/2) × 12 × 5 + (1/2) × 12 × 5 = 60 cm²
Question 2 :
The length of a tangent drawn from a point at a distance of 10 cm of circle is 8 cm. The radius of the circle is
(a) 4 cm
(b) 5 cm
(c) 6 cm
(d) 7 cm
Correct Answer – (C)
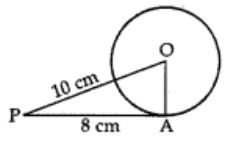
Reason: In rt. AOAP, we have
OA² + AP² = OP²
⇒ OA² + (8)² = (10)2
⇒ OA² + 64 = 100
⇒ OA² = 100 – 64 = 36
∴ OA = √36 = 6 cm
Question 3 :
The tangents drawn at the extremities of the diameter of a circle are
(a) perpendicular
(b) parallel
(c) equal
(d) none of these
Correct Answer – (B)
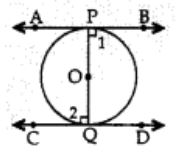
Reason: Since OP ⊥ AB and OQ ⊥ CD
∴ Z1 = 90° and Z2 = 90°
⇒ ∠1 = Z2, which are alternate angles.
∴ AB || CD
Question 4 :
The length of tangents drawn from an external point to the circle
(a) are equal
(b) are not equal
(c) sometimes are equal
(d) are not defined
Correct Answer – (A)
Question 5 :
In the given figure, if ZRPS = 25°, the value of ZROS is
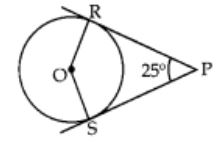
(a) 135°
(b) 145°
(c) 165°
(d) 155°
Correct Answer – (D)
∴ ∠ORP = ∠OSP = 90°
In □ ORPS, ∠ROS + ∠ORP + ∠RPS + ∠OSP = 360°
∠ROS + 90° + 25° + 90° = 360°
∠ROS = 360° – 205° = 155°
Question 6 :
In given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is
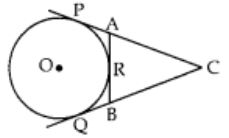
(a) 6 cm
(b) 5 cm
(c) 4 cm
(d) 3 cm
Correct Answer – (B)
BQ = BR …(i) [∵ Tangents drawn from external points are equal]
CQ = CP …[Using (i)]
BC + BQ = 11
⇒ 6 + BR = 11
⇒ BR = 11 – 6 = 5 cm
Question 7 :
Tangents from an external point to a circle are
(a) equal
(b) not equal
(c) parallel
(d) perpendicular
Correct Answer – (A)
Question 8 :
Number of tangents drawn at a point of the , circle is/are
(a) one
(b) two
(c) none
(d) infinite
Correct Answer – (A)
Question 9 :
A tangent is drawn from a point at a distance of 17 cm of circle C(0, r) of radius 8 cm. The length of its tangent is
(a) 5 cm
(b) 9 cm
(c) 15 cm
(d) 23 cm
Correct Answer – (C)
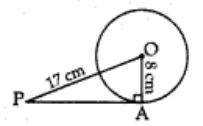
Reason: In rt ∆OAP, AP² + OA² = OP²
⇒ AP² + (8)² = (17)² => AP² + 64 = 289
⇒ AP² = 289 – 64 = 225
∴ AP = √225 = 15 cm
Question 10 :
The distance between two parallel tangents of a circle of radius 4 cm is
(a) 2 cm
(b) 4 cm
(c) 6 cm
(d) 8 cm
Correct Answer – (D)
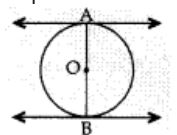
Reason: Here radius, r = 4 cm
Required distance,
AB = OA + OB
= r + r = 2r = 2×4 = 8 cm



