Multiple Choice Questions - Set - 2
Question 1:
In the figure PA and PB are tangents to the circle with centre O. If ∠APB = 60°, then ∠OAB is
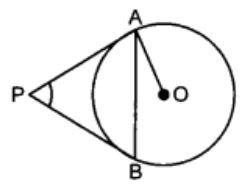
(a) 30°
(b) 60°
(c) 90°
(d) 15°
Correct Answer – (A)
∵ ∠APB + ∠PAB + ∠PBA = 180°
⇒ APB + x + x = 180°
[∵ PA = PB ∴ ∠PAB = ∠PBA = x (say)]
⇒ 60° + 2x = 180°
⇒ 2x = 180° – 60°
⇒ 2x = 120°
⇒ x = 120/2 = 60°
Also, ∠OAP = 90°
⇒ ∠OAB + ∠PAB = 90°
⇒ ∠OAB + 60°= 90°
⇒ ∠OAB = 30°
Question 2 :
In figure if O is centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to
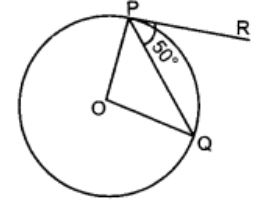
(a) 100°
(b) 80°
(c) 90°
(d) 75°
Correct Answer – (A)
∠OPQ = 90° – 50° = 40°
OP = OQ [Radii]
∴ ∠OPQ = ∠OQP = 40°
In ∆OPQ,
⇒ ∠POQ + ∠OPQ + ∠OQP = 180°
⇒ ∠POQ + 40° + 40° = 180°
∠POQ = 180° – 80° = 100°.
Question 3 :
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
(a) 60 cm²
(b) 65 cm²
(c) 30 cm²
(d) 32.5 cm²
Correct Answer – (A)
Question 4 :
C (O, r1) and C(O, r2) are two concentric circles with r1 > r2 AB is a chord of C(O, r1) touching C(O, r,2) at C then
(a) AB = r1
(b) AB = r2
(c) AC = BC
(d) AB = r1 + r2
Correct Answer – (C)
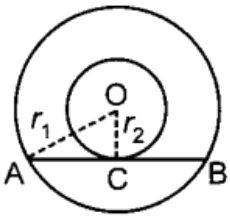
C(0, r2)
∴ OC ⊥ AB
∴ AC = BC
Question 5 :
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is
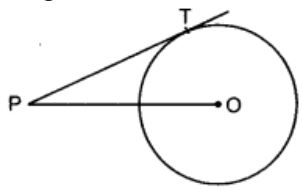
(a) 25 cm
(b) 26 cm
(c) 24 cm
(d) 10 cm
Correct Answer – (D)
Now, in AOTP,
⇒ OP² = PT² + OT²
⇒ 26² = 24² + OT²
⇒ 676 – 576 = OT²
⇒ 100 = OT²
⇒ 10 cm = OT
Question 6 :
In figure, O is the centre of a circle, AB is a chord and AT is the tangent at A. If ∠AOB = 100°, then ∠BAT is equal to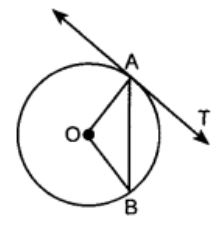
(a) 100°
(b) 40°
(c) 50°
(d) 90°
Correct Answer – (C)
∠OAB = ∠OBA (∵ OA and OB are radii)
Now, in ∆AOB,
∠AOB + ∠OAB + ∠OBA = 180°
(Angle sum property of A)
⇒ 100° + x + x = 180° [Let ∠OAB = ∠OBA = x]
⇒ 2x = 180° – 100°
⇒ 2x = 80°
⇒ x = 40°
Also, ∠OAB + ∠BAT = 90°
[∵ OA is radius and TA is tangent at A]
⇒ 40° + ZBAT = 90°
⇒ ∠BAT = 50°
Question 7 :
n figure AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to
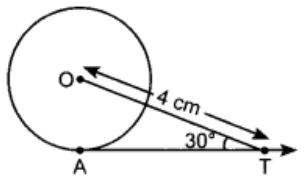
(a) 4 cm
(b) 2 cm
(c) 2√3 cm
(d) 4√3 cm
Correct Answer – (C)
Question 8 :
Two parallel lines touch the circle at points A and B respectively. If area of the circle is 25 n cm2, then AB is equal to
(a) 5 cm
(b) 8 cm
(c) 10 cm
(d) 25 cm
Correct Answer – (C)
∴ πR² = 25π
⇒ R = 5 cm
∴ Distance between two parallel tangents = diameter = 2 × 5 = 10 cm.
Question 9 :
A line through point of contact and passing through centre of circle is known as
(a) tangent
(b) chord
(c) normal
(d) segment
Correct Answer – (C)
Question 10 :
In the given figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°, then ∠BOC is equal to
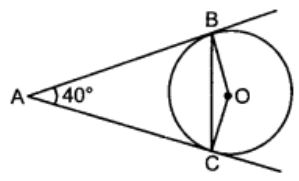
(a) 40°
(b) 50°
(c) 140°
(d) 150°
Correct Answer – (C)
∠ABO + ∠BOC + ∠OCA + ∠BAC = 360°
⇒ 90° + ∠BOC + 90° + 40° = 360°
⇒ ∠BOC = 360° – 220° = 140°



